| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 13 (Before Exercise 15.1) | Exercise 15.1 | Exercise 15.2 (Optional) |
Chapter 15 Probability
This solutions guide navigates Chapter 15: Probability, formally delving into the mathematical framework for quantifying uncertainty and randomness. While earlier introductions might have touched upon probability based on observed frequencies (empirical probability), this chapter primarily solidifies the concept of theoretical probability, often referred to as classical probability. This approach calculates the likelihood of events based on logical reasoning and the assumed symmetry of the experiment, rather than relying on data from repeated trials. It provides a powerful predictive tool for situations where the underlying possibilities can be clearly defined and are considered equally likely to occur, such as in games of chance (coins, dice, cards) or idealized selection processes. Understanding theoretical probability allows us to make calculated predictions about outcomes before an experiment is even performed, forming the basis for statistical inference and risk assessment in numerous fields.
The cornerstone of classical probability rests on the assumption of equally likely outcomes – meaning each possible outcome of a random experiment has the same chance of occurring. Under this crucial assumption, the theoretical probability of a specific event $E$ occurring is defined as the ratio of the number of outcomes that are favorable to event $E$ to the total number of possible outcomes in the experiment's sample space ($S$). Mathematically, this is expressed as:
$P(E) = \frac{\text{Number of outcomes favorable to E}}{\text{Total number of possible outcomes}} = \frac{n(E)}{n(S)}$
The solutions meticulously guide users through applying this definition, emphasizing the importance of first identifying all possible outcomes (the sample space, $S$) and then identifying the specific outcomes that constitute the event of interest ($E$).
Several fundamental properties of probability, deriving directly from this definition, are reinforced:
- The probability of any event $E$ is always a number between 0 and 1, inclusive: $0 \leq P(E) \leq 1$. This is because the number of favorable outcomes can range from zero up to the total number of outcomes.
- The probability of a sure event (an event that includes all possible outcomes, i.e., the entire sample space) is 1. ($P(S)=1$)
- The probability of an impossible event (an event with no favorable outcomes, i.e., the empty set $\emptyset$) is 0. ($P(\emptyset)=0$)
- An elementary event is an event consisting of only a single outcome in the sample space. The sum of the probabilities of all distinct elementary events that make up the sample space must equal 1. ($\Sigma P(e_i) = 1$)
A particularly useful concept explored is that of Complementary Events. For any event $E$, its complement, denoted as 'not $E$', $\bar{E}$, or $E'$, consists of all outcomes in the sample space that are not in $E$. Since an outcome must either be in $E$ or in $\bar{E}$, their probabilities sum to 1: $P(E) + P(\bar{E}) = 1$. The solutions frequently demonstrate the utility of this relationship, as it is sometimes easier to calculate $P(\bar{E})$ and then find $P(E) = 1 - P(\bar{E})$, or vice versa.
The solutions provide extensive practice problems centered around common random experiments where the assumption of equally likely outcomes is typically applied:
- Tossing fair coins (one, two, or three): Calculating probabilities for specific sequences (e.g., HHT) or counts (e.g., exactly two heads).
- Rolling fair dice (one or two): Determining probabilities for specific numbers, sums (e.g., sum is 7), products, or categories (e.g., getting a prime number, an even sum).
- Drawing cards from a standard, well-shuffled deck of 52: Finding probabilities related to suits (hearts, diamonds, clubs, spades), ranks (Ace, King, Queen, Jack, numbers), colors (red, black), or types (face cards).
- Selecting objects at random: Problems involving drawing balls of different colors from a bag or selecting numbers from a given set without bias.
- Less commonly, situations involving geometric probability might be introduced, where probability is determined by comparing areas or lengths (e.g., probability of a dart hitting a specific ring on a circular target).
For each problem type, the solutions emphasize a systematic approach: clearly defining and listing (or counting) the total possible outcomes in the sample space, carefully identifying and counting the favorable outcomes corresponding to the specific event described, and then computing the probability as the ratio $\frac{n(E)}{n(S)}$. This rigorous application reinforces the core principles of theoretical probability.
Example 1 to 13 (Before Exercise 15.1)
Example 1. Find the probability of getting a head when a coin is tossed once. Also find the probability of getting a tail.
Answer:
Given:
An experiment where a single, fair coin is tossed once.
To Find:
1. The probability of getting a Head, P(H).
2. The probability of getting a Tail, P(T).
Solution:
When a coin is tossed once, the set of all possible outcomes, known as the sample space ($S$), is:
$S = \{\text{Head, Tail}\}$ or $S = \{H, T\}$
The total number of possible outcomes is $n(S) = 2$. Each outcome is equally likely.
The probability of an event is calculated as:
$P(\text{Event}) = \frac{\text{Number of Favourable Outcomes}}{\text{Total Number of Possible Outcomes}}$
1. Probability of getting a Head:
Let $E_H$ be the event of getting a head. The favourable outcome is $\{H\}$.
Number of favourable outcomes for a head, $n(E_H) = 1$.
$P(\text{Head}) = \frac{n(E_H)}{n(S)} = \frac{1}{2}$
2. Probability of getting a Tail:
Let $E_T$ be the event of getting a tail. The favourable outcome is $\{T\}$.
Number of favourable outcomes for a tail, $n(E_T) = 1$.
$P(\text{Tail}) = \frac{n(E_T)}{n(S)} = \frac{1}{2}$
Conclusion:
The probability of getting a head is $\frac{1}{2}$.
The probability of getting a tail is $\frac{1}{2}$.
Example 2. A bag contains a red ball, a blue ball and a yellow ball, all the balls being of the same size. Kritika takes out a ball from the bag without looking into it. What is the probability that she takes out the
(i) yellow ball?
(ii) red ball?
(iii) blue ball?
Answer:
Given:
A bag contains 1 red ball, 1 blue ball, and 1 yellow ball. All balls are identical in size, ensuring each is equally likely to be picked.
To Find:
The probability of drawing a:
(i) yellow ball
(ii) red ball
(iii) blue ball
Solution:
First, we determine the total number of possible outcomes.
Total number of balls = (Number of red balls) + (Number of blue balls) + (Number of yellow balls)
Total number of balls = $1 + 1 + 1 = 3$.
So, the total number of possible outcomes is 3.
The probability formula is $P(\text{Event}) = \frac{\text{Number of Favourable Outcomes}}{\text{Total Number of Possible Outcomes}}$.
(i) Probability of drawing a yellow ball:
Number of yellow balls = 1 (This is the number of favourable outcomes).
$P(\text{Yellow ball}) = \frac{1}{3}$
(ii) Probability of drawing a red ball:
Number of red balls = 1 (This is the number of favourable outcomes).
$P(\text{Red ball}) = \frac{1}{3}$
(iii) Probability of drawing a blue ball:
Number of blue balls = 1 (This is the number of favourable outcomes).
$P(\text{Blue ball}) = \frac{1}{3}$
Since each event is elementary and equally likely, they all have the same probability.
Example 3. Suppose we throw a die once.
(i) What is the probability of getting a number greater than 4 ?
(ii) What is the probability of getting a number less than or equal to 4 ?
Answer:
Given:
A standard six-sided die is thrown once.
To Find:
(i) The probability of getting a number greater than 4.
(ii) The probability of getting a number less than or equal to 4.
Solution:
The sample space ($S$) for a single die roll is $S = \{1, 2, 3, 4, 5, 6\}$.
Total number of possible outcomes, $n(S) = 6$.
(i) Probability of getting a number greater than 4:
Let $E_1$ be the event of getting a number greater than 4.
The favourable outcomes are numbers from the sample space that are greater than 4. These are $\{5, 6\}$.
Number of favourable outcomes, $n(E_1) = 2$.
$P(E_1) = \frac{n(E_1)}{n(S)} = \frac{2}{6} = \frac{1}{3}$
(ii) Probability of getting a number less than or equal to 4:
Let $E_2$ be the event of getting a number less than or equal to 4.
The favourable outcomes are numbers from the sample space that are less than or equal to 4. These are $\{1, 2, 3, 4\}$.
Number of favourable outcomes, $n(E_2) = 4$.
$P(E_2) = \frac{n(E_2)}{n(S)} = \frac{4}{6} = \frac{2}{3}$
Note: The events $E_1$ and $E_2$ are complementary. This means $E_2$ is the same as 'not $E_1$'. We can verify this:
$P(E_1) + P(E_2) = \frac{1}{3} + \frac{2}{3} = \frac{3}{3} = 1$.
Example 4. One card is drawn from a well-shuffled deck of 52 cards. Calculate the probability that the card will
(i) be an ace,
(ii) not be an ace.
Answer:
Given:
A card is drawn at random from a standard, well-shuffled deck of 52 cards.
To Find:
(i) The probability of drawing an ace.
(ii) The probability of not drawing an ace.
Solution:
The total number of possible outcomes is the total number of cards in the deck, which is 52.
(i) Probability of drawing an ace:
Let $E$ be the event of drawing an ace.
A standard deck has 4 aces (one for each suit).
Number of favourable outcomes (aces) = 4.
$P(E) = \frac{\text{Number of aces}}{\text{Total number of cards}} = \frac{4}{52}$
Simplifying the fraction: $P(E) = \frac{1}{13}$.
(ii) Probability of not drawing an ace:
Let $E'$ be the event of not drawing an ace. This is the complementary event to $E$.
The probability of a complementary event is given by $P(E') = 1 - P(E)$.
$P(\text{not an ace}) = 1 - P(\text{an ace})$
$P(\text{not an ace}) = 1 - \frac{1}{13} = \frac{13}{13} - \frac{1}{13} = \frac{12}{13}$.
Alternate Method for (ii):
Number of cards that are not aces = Total cards - Number of aces = $52 - 4 = 48$.
$P(\text{not an ace}) = \frac{\text{Number of non-ace cards}}{\text{Total number of cards}} = \frac{48}{52}$
Simplifying by dividing numerator and denominator by 4: $P(\text{not an ace}) = \frac{12}{13}$.
Example 5. Two players, Sangeeta and Reshma, play a tennis match. It is known that the probability of Sangeeta winning the match is 0.62. What is the probability of Reshma winning the match?
Answer:
Given:
Let S be the event that Sangeeta wins the match. $P(S) = 0.62$.
Let R be the event that Reshma wins the match.
To Find:
The probability that Reshma wins the match, $P(R)$.
Solution:
In a tennis match between two players, there are only two possible outcomes: either Sangeeta wins or Reshma wins. (We assume a draw is not possible).
Therefore, the events 'Sangeeta wins' and 'Reshma wins' are complementary events.
The sum of the probabilities of complementary events is always 1.
$P(S) + P(R) = 1$
We are given $P(S) = 0.62$. Substituting this into the equation:
$0.62 + P(R) = 1$
To find $P(R)$, we rearrange the equation:
$P(R) = 1 - 0.62$
$P(R) = 0.38$
Conclusion:
The probability of Reshma winning the match is 0.38.
Example 6. Savita and Hamida are friends. What is the probability that both will have
(i) different birthdays?
(ii) the same birthday? (ignoring a leap year).
Answer:
Given:
Two friends, Savita and Hamida. We consider a non-leap year with 365 days.
To Find:
(i) The probability of them having different birthdays.
(ii) The probability of them having the same birthday.
Solution:
It is easier to first calculate the probability of them having the same birthday.
(ii) Probability of the same birthday:
Let's fix Savita's birthday. It can be any one of the 365 days of the year.
For Hamida to have the same birthday, her birthday must fall on that specific day.
Number of favourable days for Hamida's birthday = 1.
Total possible days for Hamida's birthday = 365.
$P(\text{same birthday}) = \frac{\text{Favourable outcomes}}{\text{Total outcomes}} = \frac{1}{365}$
(i) Probability of different birthdays:
The event 'having different birthdays' is the complement of the event 'having the same birthday'.
Therefore, we can use the rule of complementary events: $P(\text{Event}) = 1 - P(\text{not Event})$.
$P(\text{different birthdays}) = 1 - P(\text{same birthday})$
$P(\text{different birthdays}) = 1 - \frac{1}{365}$
$P(\text{different birthdays}) = \frac{365}{365} - \frac{1}{365} = \frac{364}{365}$
Conclusion:
(i) The probability that they have different birthdays is $\mathbf{\frac{364}{365}}$.
(ii) The probability that they have the same birthday is $\mathbf{\frac{1}{365}}$.
Example 7. There are 40 students in Class X of a school of whom 25 are girls and 15 are boys. The class teacher has to select one student as a class representative. She writes the name of each student on a separate card, the cards being identical. Then she puts cards in a bag and stirs them thoroughly. She then draws one card from the bag. What is the probability that the name written on the card is the name of
(i) a girl?
(ii) a boy?
Answer:
Given:
- Total number of students = 40.
- Number of girls = 25.
- Number of boys = 15.
One student is selected at random to be the class representative.
To Find:
(i) The probability that the selected student is a girl.
(ii) The probability that the selected student is a boy.
Solution:
The total number of possible outcomes is the total number of students, which is 40.
(i) Probability of selecting a girl:
The number of favourable outcomes is the number of girls.
Number of favourable outcomes (girls) = 25.
$P(\text{girl}) = \frac{\text{Number of girls}}{\text{Total number of students}} = \frac{25}{40}$
Simplifying the fraction by dividing the numerator and denominator by 5:
$P(\text{girl}) = \frac{5}{8}$
(ii) Probability of selecting a boy:
The number of favourable outcomes is the number of boys.
Number of favourable outcomes (boys) = 15.
$P(\text{boy}) = \frac{\text{Number of boys}}{\text{Total number of students}} = \frac{15}{40}$
Simplifying the fraction by dividing the numerator and denominator by 5:
$P(\text{boy}) = \frac{3}{8}$
Check: The events are complementary, so their probabilities should sum to 1.
$P(\text{girl}) + P(\text{boy}) = \frac{5}{8} + \frac{3}{8} = \frac{8}{8} = 1$. The calculation is correct.
Example 8. A box contains 3 blue, 2 white, and 4 red marbles. If a marble is drawn at random from the box, what is the probability that it will be
(i) white?
(ii) blue?
(iii) red?
Answer:
Given:
A box contains:
- 3 blue marbles
- 2 white marbles
- 4 red marbles
To Find:
The probability of drawing a marble that is:
(i) white
(ii) blue
(iii) red
Solution:
First, calculate the total number of marbles in the box.
Total number of marbles = $3 (\text{blue}) + 2 (\text{white}) + 4 (\text{red}) = 9$.
The total number of possible outcomes is 9.
(i) Probability of drawing a white marble:
Number of white marbles = 2 (favourable outcomes).
$P(\text{white}) = \frac{\text{Number of white marbles}}{\text{Total number of marbles}} = \frac{2}{9}$
(ii) Probability of drawing a blue marble:
Number of blue marbles = 3 (favourable outcomes).
$P(\text{blue}) = \frac{\text{Number of blue marbles}}{\text{Total number of marbles}} = \frac{3}{9} = \frac{1}{3}$
(iii) Probability of drawing a red marble:
Number of red marbles = 4 (favourable outcomes).
$P(\text{red}) = \frac{\text{Number of red marbles}}{\text{Total number of marbles}} = \frac{4}{9}$
Example 9. Harpreet tosses two different coins simultaneously (say, one is of ₹1 and other of ₹ 2). What is the probability that she gets at least one head?
Answer:
Given:
Two different coins are tossed simultaneously.
To Find:
The probability of getting at least one head.
Solution:
Step 1: Determine the sample space.
Let H represent a Head and T represent a Tail. When two coins are tossed, the possible outcomes are:
- Head on both coins (HH)
- Head on the first coin, Tail on the second (HT)
- Tail on the first coin, Head on the second (TH)
- Tail on both coins (TT)
The sample space is $S = \{\text{HH, HT, TH, TT}\}$.
The total number of possible outcomes is 4.
Step 2: Identify the favourable outcomes.
The event is "getting at least one head". This means one head or two heads.
The outcomes from the sample space that satisfy this condition are: {HH, HT, TH}.
The number of favourable outcomes is 3.
Step 3: Calculate the probability.
$P(\text{at least one head}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}} = \frac{3}{4}$
Alternate Solution (Using Complementary Event):
The complementary event to "at least one head" is "no heads".
The event "no heads" means getting tails on both coins, which is the outcome {TT}.
The probability of getting no heads is $P(\text{no heads}) = \frac{1}{4}$.
The probability of "at least one head" is 1 minus the probability of its complement.
$P(\text{at least one head}) = 1 - P(\text{no heads}) = 1 - \frac{1}{4} = \frac{3}{4}$.
Answer:
The probability that Harpreet gets at least one head is $\mathbf{\frac{3}{4}}$.
Example 10. In a musical chair game, the person playing the music has been advised to stop playing the music at any time within 2 minutes after she starts playing. What is the probability that the music will stop within the first half-minute after starting?
Answer:
Given:
The music can stop at any random time within a total period of 2 minutes.
To Find:
The probability that the music stops within the first half-minute (0.5 minutes).
Solution:
This problem deals with geometric probability, where outcomes are continuous over an interval.
The total duration in which the music can stop represents the total possible outcomes.
Total possible duration = 2 minutes.
The duration within which we want the music to stop is the favourable outcome.
Favourable duration = The first half-minute = 0.5 minutes.
The probability is the ratio of the length of the favourable duration to the length of the total possible duration.
$P(\text{Event}) = \frac{\text{Length of Favourable Interval}}{\text{Length of Total Interval}}$
$P(\text{stops in first half-minute}) = \frac{0.5 \text{ minutes}}{2 \text{ minutes}}$
$P(\text{stops in first half-minute}) = \frac{0.5}{2} = \frac{1/2}{2} = \frac{1}{4}$
Answer:
The probability that the music will stop within the first half-minute is $\mathbf{\frac{1}{4}}$ or $\mathbf{0.25}$.
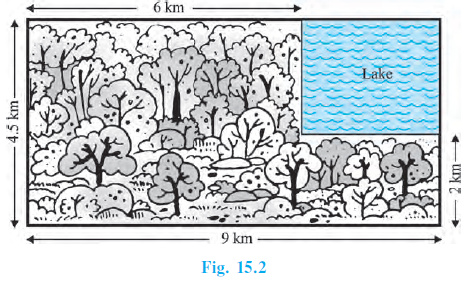
Example 11. A missing helicopter is reported to have crashed somewhere in the rectangular region shown in Fig. 15.2. What is the probability that it crashed inside the lake shown in the figure?
Answer:
Given:
A helicopter crashed somewhere in the rectangular region shown in the figure.
From the figure, the dimensions of the entire rectangular region are:
Length = 9 km
Width = 4.5 km
To Find:
The probability that the helicopter crashed inside the lake shown in the figure.
Solution:
This is a problem of geometric probability. The probability that the helicopter crashed inside the lake is the ratio of the area of the lake to the total area of the rectangular region where the helicopter could have crashed.
$P(\text{crashed in lake}) = \frac{\text{Area of the lake}}{\text{Total area of the rectangular region}}$
Step 1: Calculate the total area of the rectangular region.
Total Area = Length $\times$ Width
Total Area = $9 \text{ km} \times 4.5 \text{ km}$
Total Area = $40.5 \text{ km}^2$
Step 2: Calculate the dimensions and area of the lake.
From the figure, we can determine the length and width of the rectangular lake.
Length of the lake = (Total length of the region) - (Length of the forest region to the left of the lake)
Length of the lake = $9 \text{ km} - 6 \text{ km} = 3 \text{ km}$
Width of the lake = (Total width of the region) - (Width of the forest region below the lake)
Width of the lake = $4.5 \text{ km} - 2 \text{ km} = 2.5 \text{ km}$
Now, we can find the area of the lake.
Area of the lake = Length of the lake $\times$ Width of the lake
Area of the lake = $3 \text{ km} \times 2.5 \text{ km}$
Area of the lake = $7.5 \text{ km}^2$
Step 3: Calculate the probability.
$P(\text{crashed in lake}) = \frac{\text{Area of the lake}}{\text{Total Area}}$
$P(\text{crashed in lake}) = \frac{7.5 \text{ km}^2}{40.5 \text{ km}^2}$
To simplify the fraction, we can multiply the numerator and denominator by 10 to remove the decimals.
$P(\text{crashed in lake}) = \frac{7.5 \times 10}{40.5 \times 10} = \frac{75}{405}$
Now, we simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor. Let's start by dividing by 5.
$P(\text{crashed in lake}) = \frac{75 \div 5}{405 \div 5} = \frac{15}{81}$
Now, we can divide both by 3.
$P(\text{crashed in lake}) = \frac{15 \div 3}{81 \div 3} = \frac{5}{27}$
Answer:
The probability that the helicopter crashed inside the lake is $\mathbf{\frac{5}{27}}$.
Example 12. A carton consists of 100 shirts of which 88 are good, 8 have minor defects and 4 have major defects. Jimmy, a trader, will only accept the shirts which are good, but Sujatha, another trader, will only reject the shirts which have major defects. One shirt is drawn at random from the carton. What is the probability that
(i) it is acceptable to Jimmy?
(ii) it is acceptable to Sujatha?
Answer:
Given:
- Total number of shirts = 100.
- Number of good shirts = 88.
- Number of shirts with minor defects = 8.
- Number of shirts with major defects = 4.
Acceptance Criteria:
- Jimmy: Accepts only good shirts.
- Sujatha: Rejects only shirts with major defects.
To Find:
(i) Probability that a randomly drawn shirt is acceptable to Jimmy.
(ii) Probability that a randomly drawn shirt is acceptable to Sujatha.
Solution:
The total number of possible outcomes is 100, as any of the 100 shirts can be drawn.
The probability is calculated as $P(\text{Event}) = \frac{\text{Number of Favourable Outcomes}}{\text{Total Number of Outcomes}}$.
(i) Probability of being acceptable to Jimmy:
Jimmy accepts only good shirts. The number of good shirts is the number of favourable outcomes for Jimmy.
Number of favourable outcomes = 88.
$P(\text{acceptable to Jimmy}) = \frac{88}{100}$
Simplifying the fraction gives:
$P(\text{acceptable to Jimmy}) = \frac{22}{25}$ or $0.88$.
(ii) Probability of being acceptable to Sujatha:
Sujatha accepts all shirts except those with major defects. This means she accepts good shirts and shirts with minor defects.
Number of favourable outcomes = (Number of good shirts) + (Number of shirts with minor defects)
Number of favourable outcomes = $88 + 8 = 96$.
$P(\text{acceptable to Sujatha}) = \frac{96}{100}$
Simplifying the fraction gives:
$P(\text{acceptable to Sujatha}) = \frac{24}{25}$ or $0.96$.
Answer:
(i) The probability that the shirt is acceptable to Jimmy is $\mathbf{\frac{22}{25}}$.
(ii) The probability that the shirt is acceptable to Suj-atha is $\mathbf{\frac{24}{25}}$.
Example 13. Two dice, one blue and one grey, are thrown at the same time. Write down all the possible outcomes. What is the probability that the sum of the two numbers appearing on the top of the dice is
(i) 8?
(ii) 13?
(iii) less than or equal to 12?
Answer:
Given:
Two distinct dice (one blue, one grey) are thrown simultaneously.
To Find:
1. All possible outcomes.
2. The probability that the sum of the numbers is (i) 8, (ii) 13, (iii) less than or equal to 12.
Solution:
1. All Possible Outcomes:
Each die has 6 faces numbered 1 to 6. The total number of possible outcomes is $6 \times 6 = 36$. The sample space, represented as (blue die, grey die), is:
| (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
2. Calculating Probabilities:
(i) Probability that the sum is 8:
Let $E_1$ be the event of getting a sum of 8. The favourable outcomes are:
$E_1 = \{(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)\}$.
Number of favourable outcomes = 5.
$P(\text{sum is 8}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} = \frac{5}{36}$.
(ii) Probability that the sum is 13:
Let $E_2$ be the event of getting a sum of 13. The maximum possible sum from two dice is $6 + 6 = 12$. Therefore, it is impossible to get a sum of 13.
Number of favourable outcomes = 0.
$P(\text{sum is 13}) = \frac{0}{36} = 0$. This is an impossible event.
(iii) Probability that the sum is less than or equal to 12:
Let $E_3$ be the event of getting a sum less than or equal to 12. As established, the minimum sum is $1+1=2$ and the maximum sum is $6+6=12$. All 36 possible outcomes will result in a sum that is less than or equal to 12.
Number of favourable outcomes = 36.
$P(\text{sum} \leq 12) = \frac{36}{36} = 1$. This is a certain event.
Exercise 15.1
Question 1. Complete the following statements:
(i) Probability of an event E + Probability of the event ‘not E’ = _____________.
(ii) The probability of an event that cannot happen is ________________. Such an event is called .
(iii) The probability of an event that is certain to happen is _________________. Such an event is called .
(iv) The sum of the probabilities of all the elementary events of an experiment is ________________.
(v) The probability of an event is greater than or equal to _______________and less than or equal to .
Answer:
(i) Probability of an event E + Probability of the event ‘not E’ = $\mathbf{1}$.
(ii) The probability of an event that cannot happen is $\mathbf{0}$. Such an event is called $\mathbf{impossible \ event}$.
(iii) The probability of an event that is certain to happen is $\mathbf{1}$. Such an event is called $\mathbf{sure \ event}$ or $\mathbf{certain \ event}$.
(iv) The sum of the probabilities of all the elementary events of an experiment is $\mathbf{1}$.
(v) The probability of an event is greater than or equal to $\mathbf{0}$ and less than or equal to $\mathbf{1}$.
Question 2. Which of the following experiments have equally likely outcomes? Explain.
(i) A driver attempts to start a car. The car starts or does not start.
(ii) A player attempts to shoot a basketball. She/he shoots or misses the shot.
(iii) A trial is made to answer a true-false question. The answer is right or wrong.
(iv) A baby is born. It is a boy or a girl.
Answer:
(i) Not equally likely outcomes.
The probability of a car starting or not starting depends on various factors such as the car's condition, fuel level, battery status, etc. These factors can make one outcome (starting) more or less likely than the other (not starting).
(ii) Not equally likely outcomes.
The probability of a player shooting or missing a basketball shot depends on the player's skill level, distance from the basket, presence of defenders, etc. A skilled player is more likely to make the shot than a beginner, so the outcomes are not equally likely in general.
(iii) Equally likely outcomes.
Assuming the question is a standard true-false question and there is no prior knowledge influencing the answer, there are only two possible outcomes: the answer is either right or wrong. When a trial is made (implying a choice or guess without bias), each outcome has an equal chance of occurring.
(iv) Equally likely outcomes.
While there are minor biological variations that cause a slight difference in the birth rate of boys and girls globally, for the purpose of a standard probability problem at this level, the outcomes of a baby being born a boy or a girl are considered to be equally likely. Each outcome has a probability of approximately $\frac{1}{2}$.
Question 3. Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of a football game?
Answer:
Tossing a coin is considered a fair way of deciding which team should get the ball at the beginning of a football game because the outcome of a coin toss is **equally likely** for both possibilities.
When a standard, unbiased coin is tossed, there are only two possible outcomes: getting a Head (H) or getting a Tail (T).
The probability of getting a Head is $\frac{1}{2}$.
The probability of getting a Tail is $\frac{1}{2}$.
Since $P(\text{Head}) = P(\text{Tail}) = \frac{1}{2}$, both outcomes are equally likely. This means that each team has an equal chance of winning the toss (assuming one team chooses Heads and the other chooses Tails).
Furthermore, the outcome of a coin toss is unpredictable and random, as there is no way to influence or predict the result of a single toss.
Because each team has an equal probability of winning the toss, it provides a neutral and unbiased method for making the decision, ensuring fairness at the start of the game.
Question 4. Which of the following cannot be the probability of an event?
(A) $\frac{2}{3}$
(B) –1.5
(C) 15%
(D) 0.7
Answer:
Solution:
The probability of any event E, denoted by $P(E)$, must satisfy the condition:
$0 \leq P(E) \leq 1$
Let's examine each option:
(A) $\frac{2}{3}$
This is a fraction. $\frac{2}{3} \approx 0.667$.
Since $0 \leq 0.667 \leq 1$, this value can be a probability.
(B) –1.5
This is a negative number.
The probability of an event cannot be negative.
Since $-1.5 < 0$, this value cannot be a probability.
(C) 15%
This is a percentage. We can convert it to a decimal:
$15\% = \frac{15}{100} = 0.15$
Since $0 \leq 0.15 \leq 1$, this value can be a probability.
(D) 0.7
This is a decimal number.
Since $0 \leq 0.7 \leq 1$, this value can be a probability.
Based on the property that the probability of an event must be between 0 and 1 (inclusive), the value –1.5 is the only option that falls outside this range.
Answer:
The option that cannot be the probability of an event is $\mathbf{(B) \ –1.5}$.
Question 5. If P(E) = 0.05, what is the probability of ‘not E’?
Answer:
Given:
The probability of event E is $P(E) = 0.05$.
To Find:
The probability of the event 'not E', often denoted as $P(\text{not } E)$ or $P(\bar{E})$.
Solution:
For any event E, the event 'not E' is the complementary event. This means that event E and event 'not E' are mutually exclusive and exhaustive.
The sum of the probability of an event and the probability of its complementary event is always equal to 1.
The relationship is given by the formula:
$P(E) + P(\text{not } E) = 1$
We are given that $P(E) = 0.05$. Substitute this value into the formula:
$0.05 + P(\text{not } E) = 1$
To find $P(\text{not } E)$, subtract 0.05 from both sides of the equation:
$P(\text{not } E) = 1 - 0.05$
Calculating the subtraction:
$P(\text{not } E) = 0.95$
Answer:
The probability of ‘not E’ is $\mathbf{0.95}$.
Question 6. A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out
(i) an orange flavoured candy?
(ii) a lemon flavoured candy?
Answer:
Given:
A bag contains only lemon flavoured candies.
Malini takes out one candy at random.
To Find:
(i) The probability that she takes out an orange flavoured candy.
(ii) The probability that she takes out a lemon flavoured candy.
Solution:
Let $N$ be the total number of candies in the bag. Since the bag contains only lemon flavoured candies, all $N$ candies are lemon flavoured.
Total number of possible outcomes when drawing one candy = $N$.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability of taking out an orange flavoured candy:
The event is drawing an orange flavoured candy.
Since the bag contains only lemon flavoured candies, there are no orange flavoured candies in the bag.
Number of favourable outcomes (orange) = 0.
The probability of drawing an orange flavoured candy is:
$P(\text{orange}) = \frac{\text{Number of orange candies}}{\text{Total number of candies}}$
$P(\text{orange}) = \frac{0}{N}$
$P(\text{orange}) = 0$
This is an impossible event.
(ii) Probability of taking out a lemon flavoured candy:
The event is drawing a lemon flavoured candy.
Since the bag contains only lemon flavoured candies, every candy in the bag is a lemon flavoured candy.
Number of favourable outcomes (lemon) = Total number of candies = $N$.
The probability of drawing a lemon flavoured candy is:
$P(\text{lemon}) = \frac{\text{Number of lemon candies}}{\text{Total number of candies}}$
$P(\text{lemon}) = \frac{N}{N}$
$P(\text{lemon}) = 1$
This is a certain event.
Answer:
(i) The probability that she takes out an orange flavoured candy is $\mathbf{0}$.
(ii) The probability that she takes out a lemon flavoured candy is $\mathbf{1}$.
Question 7. It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
Answer:
Given:
The probability that 2 students do not have the same birthday, $P(\text{not having same birthday}) = 0.992$.
To Find:
The probability that the 2 students have the same birthday.
Solution:
Let E be the event that 2 students have the same birthday.
Let $\bar{E}$ be the event that 2 students do not have the same birthday.
The events E and $\bar{E}$ are complementary events. This means that the sum of their probabilities is 1.
$P(E) + P(\bar{E}) = 1$
We are given $P(\bar{E}) = 0.992$.
Substitute the given value into the equation:
$P(E) + 0.992 = 1$
To find $P(E)$, subtract 0.992 from both sides of the equation:
$P(E) = 1 - 0.992$
Calculating the subtraction:
$P(E) = 0.008$
Answer:
The probability that the 2 students have the same birthday is $\mathbf{0.008}$.
Question 8. A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is
(i) red ?
(ii) not red?
Answer:
Given:
Number of red balls = 3.
Number of black balls = 5.
A ball is drawn at random from the bag.
To Find:
(i) The probability that the ball drawn is red.
(ii) The probability that the ball drawn is not red.
Solution:
First, calculate the total number of balls in the bag.
Total number of balls = Number of red balls + Number of black balls
Total number of balls = $3 + 5 = 8$.
When a ball is drawn at random, the total number of possible outcomes is the total number of balls, which is 8.
Total number of possible outcomes = 8.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability that the ball drawn is red:
The event is drawing a red ball.
The number of favourable outcomes for this event is the number of red balls.
Number of favourable outcomes (red) = 3.
The probability of drawing a red ball is:
$P(\text{red}) = \frac{\text{Number of red balls}}{\text{Total number of balls}}$
$P(\text{red}) = \frac{3}{8}$
(ii) Probability that the ball drawn is not red:
The event 'not red' means drawing a ball that is not red.
In this bag, the balls that are not red are the black balls.
Number of favourable outcomes (not red) = Number of black balls = 5.
The probability of drawing a ball that is not red is:
$P(\text{not red}) = \frac{\text{Number of black balls}}{\text{Total number of balls}}$
$P(\text{not red}) = \frac{5}{8}$
Alternate Solution for (ii):
The event "drawing a red ball" and the event "drawing a ball that is not red" are complementary events. This means that one event must happen if the other does not.
For any event E, $P(\text{not } E) = 1 - P(E)$.
Here, $P(\text{not red}) = 1 - P(\text{red})$.
From part (i), we found $P(\text{red}) = \frac{3}{8}$.
So, $P(\text{not red}) = 1 - \frac{3}{8}$
$P(\text{not red}) = \frac{8}{8} - \frac{3}{8}$
$P(\text{not red}) = \frac{8-3}{8}$
$P(\text{not red}) = \frac{5}{8}$
This confirms the result obtained earlier.
Answer:
(i) The probability that the ball drawn is red is $\mathbf{\frac{3}{8}}$.
(ii) The probability that the ball drawn is not red is $\mathbf{\frac{5}{8}}$.
Question 9. A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be
(i) red ?
(ii) white ?
(iii) not green?
Answer:
Given:
Number of red marbles = 5.
Number of white marbles = 8.
Number of green marbles = 4.
To Find:
(i) Probability of drawing a red marble.
(ii) Probability of drawing a white marble.
(iii) Probability of drawing a marble that is not green.
Solution:
First, calculate the total number of marbles in the box.
Total number of marbles = Number of red marbles + Number of white marbles + Number of green marbles
Total number of marbles = $5 + 8 + 4 = 17$.
When a marble is taken out at random, the total number of possible outcomes is the total number of marbles, which is 17.
Total number of possible outcomes = 17.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability of drawing a red marble:
The event is drawing a red marble.
The number of favourable outcomes for this event is the number of red marbles.
Number of favourable outcomes (red) = 5.
The probability of drawing a red marble is:
$P(\text{red}) = \frac{\text{Number of red marbles}}{\text{Total number of marbles}}$
$P(\text{red}) = \frac{5}{17}$
(ii) Probability of drawing a white marble:
The event is drawing a white marble.
The number of favourable outcomes for this event is the number of white marbles.
Number of favourable outcomes (white) = 8.
The probability of drawing a white marble is:
$P(\text{white}) = \frac{\text{Number of white marbles}}{\text{Total number of marbles}}$
$P(\text{white}) = \frac{8}{17}$
(iii) Probability of drawing a marble that is not green:
The event 'not green' means drawing a marble that is either red or white.
The number of marbles that are not green = Number of red marbles + Number of white marbles
Number of favourable outcomes (not green) = $5 + 8 = 13$.
The probability of drawing a marble that is not green is:
$P(\text{not green}) = \frac{\text{Number of marbles that are not green}}{\text{Total number of marbles}}$
$P(\text{not green}) = \frac{13}{17}$
Alternate Solution for (iii):
The event "drawing a green marble" and the event "drawing a marble that is not green" are complementary events.
First, calculate the probability of drawing a green marble:
$P(\text{green}) = \frac{\text{Number of green marbles}}{\text{Total number of marbles}} = \frac{4}{17}$
Now, use the complementary event formula: $P(\text{not green}) = 1 - P(\text{green})$.
$P(\text{not green}) = 1 - \frac{4}{17}$
$P(\text{not green}) = \frac{17}{17} - \frac{4}{17}$
$P(\text{not green}) = \frac{17-4}{17}$
$P(\text{not green}) = \frac{13}{17}$
This confirms the result obtained earlier.
Answer:
(i) The probability that the marble taken out will be red is $\mathbf{\frac{5}{17}}$.
(ii) The probability that the marble taken out will be white is $\mathbf{\frac{8}{17}}$.
(iii) The probability that the marble taken out will be not green is $\mathbf{\frac{13}{17}}$.
Question 10. A piggy bank contains hundred 50p coins, fifty ₹1 coins, twenty ₹ 2 coins and ten ₹5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, what is the probability that the coin
(i) will be a 50 p coin ?
(ii) will not be a ₹ 5 coin?
Answer:
Given:
Number of 50p coins = 100.
Number of $\textsf{₹}$1 coins = 50.
Number of $\textsf{₹}$2 coins = 20.
Number of $\textsf{₹}$5 coins = 10.
To Find:
(i) Probability that the coin is a 50p coin.
(ii) Probability that the coin is not a $\textsf{₹}$5 coin.
Solution:
First, calculate the total number of coins in the piggy bank.
Total number of coins = (Number of 50p coins) + (Number of $\textsf{₹}$1 coins) + (Number of $\textsf{₹}$2 coins) + (Number of $\textsf{₹}$5 coins)
Total number of coins = $100 + 50 + 20 + 10 = 180$.
When one coin falls out, the total number of possible outcomes is 180.
Total number of possible outcomes = 180.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability that the coin will be a 50p coin:
The event is getting a 50p coin.
The number of favourable outcomes for this event is the number of 50p coins.
Number of favourable outcomes (50p) = 100.
The probability of getting a 50p coin is:
$P(\text{50p}) = \frac{\text{Number of 50p coins}}{\text{Total number of coins}}$
$P(\text{50p}) = \frac{100}{180}$
Simplify the fraction by dividing numerator and denominator by their greatest common divisor, which is 20.
$P(\text{50p}) = \frac{\cancel{100}^{5}}{\cancel{180}_{9}}$
$P(\text{50p}) = \frac{5}{9}$
(ii) Probability that the coin will not be a $\textsf{₹}$5 coin:
The event is getting a coin that is not a $\textsf{₹}$5 coin.
The coins that are not $\textsf{₹}$5 are the 50p, $\textsf{₹}$1, and $\textsf{₹}$2 coins.
Number of coins that are not $\textsf{₹}$5 = (Number of 50p coins) + (Number of $\textsf{₹}$1 coins) + (Number of $\textsf{₹}$2 coins)
Number of favourable outcomes (not $\textsf{₹}$5) = $100 + 50 + 20 = 170$.
The probability of getting a coin that is not a $\textsf{₹}$5 coin is:
$P(\text{not } \textsf{₹}5) = \frac{\text{Number of coins not } \textsf{₹}5}{\text{Total number of coins}}$
$P(\text{not } \textsf{₹}5) = \frac{170}{180}$
Simplify the fraction by dividing numerator and denominator by their greatest common divisor, which is 10.
$P(\text{not } \textsf{₹}5) = \frac{\cancel{170}^{17}}{\cancel{180}_{18}}$
$P(\text{not } \textsf{₹}5) = \frac{17}{18}$
Alternate Solution for (ii):
The event "getting a $\textsf{₹}$5 coin" and the event "getting a coin that is not a $\textsf{₹}$5 coin" are complementary events.
First, calculate the probability of getting a $\textsf{₹}$5 coin:
$P(\textsf{₹}5) = \frac{\text{Number of } \textsf{₹}5 \text{ coins}}{\text{Total number of coins}} = \frac{10}{180} = \frac{1}{18}$
Now, use the complementary event formula: $P(\text{not } \textsf{₹}5) = 1 - P(\textsf{₹}5)$.
$P(\text{not } \textsf{₹}5) = 1 - \frac{1}{18}$
$P(\text{not } \textsf{₹}5) = \frac{18}{18} - \frac{1}{18}$
$P(\text{not } \textsf{₹}5) = \frac{18-1}{18}$
$P(\text{not } \textsf{₹}5) = \frac{17}{18}$
This confirms the result obtained earlier.
Answer:
(i) The probability that the coin will be a 50p coin is $\mathbf{\frac{5}{9}}$.
(ii) The probability that the coin will not be a $\textsf{₹}$5 coin is $\mathbf{\frac{17}{18}}$.
Question 11. Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish (see Fig. 15.4). What is the probability that the fish taken out is a male fish?
Answer:
Given:
Number of male fish = 5.
Number of female fish = 8.
To Find:
The probability that the fish taken out is a male fish.
Solution:
First, calculate the total number of fish in the tank.
Total number of fish = Number of male fish + Number of female fish
Total number of fish = $5 + 8 = 13$.
When one fish is taken out at random, the total number of possible outcomes is the total number of fish, which is 13.
Total number of possible outcomes = 13.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
The event is drawing a male fish.
The number of favourable outcomes for this event is the number of male fish.
Number of favourable outcomes (male) = 5.
The probability of drawing a male fish is:
$P(\text{male fish}) = \frac{\text{Number of male fish}}{\text{Total number of fish}}$
$P(\text{male fish}) = \frac{5}{13}$
Answer:
The probability that the fish taken out is a male fish is $\mathbf{\frac{5}{13}}$.
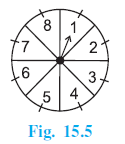
Question 12. A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see Fig. 15.5 ), and these are equally likely outcomes. What is the probability that it will point at
(i) 8 ?
(ii) an odd number?
(iii) a number greater than 2?
(iv) a number less than 9?
Answer:
Given:
An arrow is spun and comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8.
The outcomes are equally likely.
To Find:
The probability that the arrow will point at:
(i) 8
(ii) an odd number
(iii) a number greater than 2
(iv) a number less than 9
Solution:
The set of all possible outcomes when the arrow stops is the sample space S:
$S = \{1, 2, 3, 4, 5, 6, 7, 8\}$
The total number of possible outcomes is the number of elements in the sample space.
Total number of outcomes = $|S| = 8$.
Since the outcomes are equally likely, the probability of any specific outcome is $\frac{1}{8}$.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability that the arrow will point at 8:
Let E$_{1}$ be the event that the arrow points at 8.
The favourable outcome for this event is {8}.
Number of favourable outcomes for E$_{1}$ = 1.
The probability of event E$_{1}$ is:
$P(E_{1}) = P(\text{pointing at 8}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
$P(\text{pointing at 8}) = \frac{1}{8}$
(ii) Probability that the arrow will point at an odd number:
Let E$_{2}$ be the event that the arrow points at an odd number.
The odd numbers in the sample space S are {1, 3, 5, 7}.
The favourable outcomes for E$_{2}$ are {1, 3, 5, 7}.
Number of favourable outcomes for E$_{2}$ = 4.
The probability of event E$_{2}$ is:
$P(E_{2}) = P(\text{pointing at an odd number}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
$P(\text{pointing at an odd number}) = \frac{4}{8}$
Simplify the fraction by dividing numerator and denominator by 4.
$P(\text{pointing at an odd number}) = \frac{\cancel{4}^{1}}{\cancel{8}_{2}}$
$P(\text{pointing at an odd number}) = \frac{1}{2}$
(iii) Probability that the arrow will point at a number greater than 2:
Let E$_{3}$ be the event that the arrow points at a number greater than 2.
The numbers in the sample space S that are greater than 2 are {3, 4, 5, 6, 7, 8}.
The favourable outcomes for E$_{3}$ are {3, 4, 5, 6, 7, 8}.
Number of favourable outcomes for E$_{3}$ = 6.
The probability of event E$_{3}$ is:
$P(E_{3}) = \ $$ P(\text{pointing at a number greater than 2}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
$P(\text{pointing at a number greater than 2}) = \frac{6}{8}$
Simplify the fraction by dividing numerator and denominator by 2.
$P(\text{pointing at a number greater than 2}) = \frac{\cancel{6}^{3}}{\cancel{8}_{4}}$
$P(\text{pointing at a number greater than 2}) = \frac{3}{4}$
(iv) Probability that the arrow will point at a number less than 9:
Let E$_{4}$ be the event that the arrow points at a number less than 9.
The numbers in the sample space S that are less than 9 are {1, 2, 3, 4, 5, 6, 7, 8}.
All outcomes in the sample space are less than 9.
The favourable outcomes for E$_{4}$ are {1, 2, 3, 4, 5, 6, 7, 8}.
Number of favourable outcomes for E$_{4}$ = 8.
The probability of event E$_{4}$ is:
$P(E_{4}) \ $$ = P(\text{pointing at a number less than 9}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
$P(\text{pointing at a number less than 9}) = \frac{8}{8}$
$P(\text{pointing at a number less than 9}) = 1$
This is a certain event.
Answer:
(i) The probability that it will point at 8 is $\mathbf{\frac{1}{8}}$.
(ii) The probability that it will point at an odd number is $\mathbf{\frac{1}{2}}$.
(iii) The probability that it will point at a number greater than 2 is $\mathbf{\frac{3}{4}}$.
(iv) The probability that it will point at a number less than 9 is $\mathbf{1}$.
Question 13. A die is thrown once. Find the probability of getting
(i) a prime number;
(ii) a number lying between 2 and 6;
(iii) an odd number.
Answer:
Given:
A die is thrown once.
To Find:
The probability of getting:
(i) a prime number.
(ii) a number lying between 2 and 6.
(iii) an odd number.
Solution:
When a standard six-sided die is thrown once, the set of all possible outcomes is the sample space S:
$S = \{1, 2, 3, 4, 5, 6\}$
The total number of possible outcomes is the number of elements in the sample space.
Total number of outcomes = $|S| = 6$.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability of getting a prime number:
Let E$_{1}$ be the event of getting a prime number.
Prime numbers in the sample space S are numbers greater than 1 that have no positive divisors other than 1 and themselves.
The prime numbers in S are {2, 3, 5}.
The favourable outcomes for E$_{1}$ are {2, 3, 5}.
Number of favourable outcomes for E$_{1}$ = 3.
The probability of event E$_{1}$ is:
$P(E_{1}) = P(\text{prime number}) = \frac{\text{Number of prime numbers}}{\text{Total number of outcomes}}$
$P(\text{prime number}) = \frac{3}{6}$
Simplify the fraction by dividing numerator and denominator by 3.
$P(\text{prime number}) = \frac{\cancel{3}^{1}}{\cancel{6}_{2}}$
$P(\text{prime number}) = \frac{1}{2}$
(ii) Probability of getting a number lying between 2 and 6:
Let E$_{2}$ be the event of getting a number lying between 2 and 6.
The numbers in the sample space S that are strictly between 2 and 6 are {3, 4, 5}.
The favourable outcomes for E$_{2}$ are {3, 4, 5}.
Number of favourable outcomes for E$_{2}$ = 3.
The probability of event E$_{2}$ is:
$P(E_{2}) = P(\text{number between 2 and 6}) = \frac{\text{Number of outcomes between 2 and 6}}{\text{Total number of outcomes}}$
$P(\text{number between 2 and 6}) = \frac{3}{6}$
Simplify the fraction by dividing numerator and denominator by 3.
$P(\text{number between 2 and 6}) = \frac{\cancel{3}^{1}}{\cancel{6}_{2}}$
$P(\text{number between 2 and 6}) = \frac{1}{2}$
(iii) Probability of getting an odd number:
Let E$_{3}$ be the event of getting an odd number.
The odd numbers in the sample space S are {1, 3, 5}.
The favourable outcomes for E$_{3}$ are {1, 3, 5}.
Number of favourable outcomes for E$_{3}$ = 3.
The probability of event E$_{3}$ is:
$P(E_{3}) = P(\text{odd number}) = \frac{\text{Number of odd numbers}}{\text{Total number of outcomes}}$
$P(\text{odd number}) = \frac{3}{6}$
Simplify the fraction by dividing numerator and denominator by 3.
$P(\text{odd number}) = \frac{\cancel{3}^{1}}{\cancel{6}_{2}}$
$P(\text{odd number}) = \frac{1}{2}$
Answer:
(i) The probability of getting a prime number is $\mathbf{\frac{1}{2}}$.
(ii) The probability of getting a number lying between 2 and 6 is $\mathbf{\frac{1}{2}}$.
(iii) The probability of getting an odd number is $\mathbf{\frac{1}{2}}$.
Question 14. One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting
(i) a king of red colour
(ii) a face card
(iii) a red face card
(iv) the jack of hearts
(v) a spade
(vi) the queen of diamonds
Answer:
Given:
A well-shuffled deck of 52 cards.
One card is drawn at random.
To Find:
The probability of getting:
(i) a king of red colour
(ii) a face card
(iii) a red face card
(iv) the jack of hearts
(v) a spade
(vi) the queen of diamonds
Solution:
The total number of possible outcomes when drawing one card from a deck of 52 cards is 52.
Total number of possible outcomes = 52.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability of getting a king of red colour:
The red colours suits are Hearts ($\heartsuit$) and Diamonds ($\diamondsuit$).
The kings of red colour are the King of Hearts and the King of Diamonds.
Number of favourable outcomes (king of red colour) = 2.
The probability is:
$P(\text{king of red colour}) = \frac{\text{Number of kings of red colour}}{\text{Total number of cards}}$
$P(\text{king of red colour}) = \frac{2}{52}$
Simplify the fraction:
$P(\text{king of red colour}) = \frac{\cancel{2}^{1}}{\cancel{52}_{26}}$
$P(\text{king of red colour}) = \frac{1}{26}$
(ii) Probability of getting a face card:
The face cards in a deck are Jack, Queen, and King.
Each of the four suits (Hearts, Diamonds, Clubs, Spades) has 3 face cards.
Total number of face cards = $3 \times 4 = 12$.
Number of favourable outcomes (face card) = 12.
The probability is:
$P(\text{face card}) = \frac{\text{Number of face cards}}{\text{Total number of cards}}$
$P(\text{face card}) = \frac{12}{52}$
Simplify the fraction by dividing numerator and denominator by 4:
$P(\text{face card}) = \frac{\cancel{12}^{3}}{\cancel{52}_{13}}$
$P(\text{face card}) = \frac{3}{13}$
(iii) Probability of getting a red face card:
The red suits are Hearts and Diamonds.
The face cards in Hearts are Jack, Queen, King (3 cards).
The face cards in Diamonds are Jack, Queen, King (3 cards).
Total number of red face cards = $3 + 3 = 6$.
Number of favourable outcomes (red face card) = 6.
The probability is:
$P(\text{red face card}) = \frac{\text{Number of red face cards}}{\text{Total number of cards}}$
$P(\text{red face card}) = \frac{6}{52}$
Simplify the fraction by dividing numerator and denominator by 2:
$P(\text{red face card}) = \frac{\cancel{6}^{3}}{\cancel{52}_{26}}$
$P(\text{red face card}) = \frac{3}{26}$
(iv) Probability of getting the jack of hearts:
There is only one Jack of Hearts in a deck of 52 cards.
Number of favourable outcomes (jack of hearts) = 1.
The probability is:
$P(\text{jack of hearts}) = \frac{\text{Number of jack of hearts}}{\text{Total number of cards}}$
$P(\text{jack of hearts}) = \frac{1}{52}$
(v) Probability of getting a spade:
There are 13 cards of the Spade suit in a deck (Ace, 2, 3, ..., 10, Jack, Queen, King of Spades).
Number of favourable outcomes (a spade) = 13.
The probability is:
$P(\text{a spade}) = \frac{\text{Number of spades}}{\text{Total number of cards}}$
$P(\text{a spade}) = \frac{13}{52}$
Simplify the fraction by dividing numerator and denominator by 13:
$P(\text{a spade}) = \frac{\cancel{13}^{1}}{\cancel{52}_{4}}$
$P(\text{a spade}) = \frac{1}{4}$
(vi) Probability of getting the queen of diamonds:
There is only one Queen of Diamonds in a deck of 52 cards.
Number of favourable outcomes (queen of diamonds) = 1.
The probability is:
$P(\text{queen of diamonds}) = \frac{\text{Number of queen of diamonds}}{\text{Total number of cards}}$
$P(\text{queen of diamonds}) = \frac{1}{52}$
Answer:
(i) The probability of getting a king of red colour is $\mathbf{\frac{1}{26}}$.
(ii) The probability of getting a face card is $\mathbf{\frac{3}{13}}$.
(iii) The probability of getting a red face card is $\mathbf{\frac{3}{26}}$.
(iv) The probability of getting the jack of hearts is $\mathbf{\frac{1}{52}}$.
(v) The probability of getting a spade is $\mathbf{\frac{1}{4}}$.
(vi) The probability of getting the queen of diamonds is $\mathbf{\frac{1}{52}}$.
Question 15. Five cards—the ten, jack, queen, king and ace of diamonds, are well-shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen?
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is (a) an ace? (b) a queen?
Answer:
Given:
The initial set of cards is the ten, jack, queen, king, and ace of diamonds.
These 5 cards are well-shuffled, and one card is picked at random.
To Find:
(i) The probability that the first card is the queen.
(ii) If the queen is drawn and put aside, the probability that the second card picked up is (a) an ace? (b) a queen?
Solution:
The initial set of cards is $\{$10 of Diamonds, Jack of Diamonds, Queen of Diamonds, King of Diamonds, Ace of Diamonds$\}$.
The total number of cards initially is 5.
Total number of possible outcomes = 5.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability that the card is the queen:
Let E$_{1}$ be the event that the first card drawn is the queen.
There is only one Queen of Diamonds in the initial set of 5 cards.
Number of favourable outcomes for E$_{1}$ (queen) = 1.
The probability of drawing the queen is:
$P(E_{1}) = P(\text{queen}) = \frac{\text{Number of queens}}{\text{Total number of cards}}$
$P(\text{queen}) = \frac{1}{5}$
(ii) If the queen is drawn and put aside:
After drawing the queen and putting it aside, there are now only 4 cards left.
The remaining cards are $\{$10 of Diamonds, Jack of Diamonds, King of Diamonds, Ace of Diamonds$\}$.
The new total number of possible outcomes for the second draw is 4.
(ii) (a) Probability that the second card picked up is an ace:
Let E$_{2a}$ be the event that the second card drawn is an ace.
From the remaining 4 cards, there is one Ace of Diamonds.
Number of favourable outcomes for E$_{2a}$ (ace) = 1.
The probability of drawing an ace as the second card (given the queen was drawn first and put aside) is:
$P(E_{2a}) = P(\text{ace second}) = \frac{\text{Number of aces remaining}}{\text{Total number of cards remaining}}$
$P(\text{ace second}) = \frac{1}{4}$
(ii) (b) Probability that the second card picked up is a queen:
Let E$_{2b}$ be the event that the second card drawn is a queen.
Since the queen was drawn first and put aside, there are no queens left among the remaining 4 cards.
Number of favourable outcomes for E$_{2b}$ (queen) = 0.
The probability of drawing a queen as the second card (given the queen was drawn first and put aside) is:
$P(E_{2b}) = P(\text{queen second}) = \frac{\text{Number of queens remaining}}{\text{Total number of cards remaining}}$
$P(\text{queen second}) = \frac{0}{4}$
$P(\text{queen second}) = 0$
Answer:
(i) The probability that the card is the queen is $\mathbf{\frac{1}{5}}$.
(ii) If the queen is drawn and put aside:
(a) The probability that the second card picked up is an ace is $\mathbf{\frac{1}{4}}$.
(b) The probability that the second card picked up is a queen is $\mathbf{0}$.
Question 16. 12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Answer:
Given:
Number of defective pens = 12.
Number of good pens = 132.
One pen is taken out at random from the lot.
To Find:
The probability that the pen taken out is a good one.
Solution:
First, calculate the total number of pens in the lot.
Total number of pens = Number of defective pens + Number of good pens
Total number of pens = $12 + 132 = 144$.
When one pen is taken out at random, the total number of possible outcomes is the total number of pens, which is 144.
Total number of possible outcomes = 144.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
The event is drawing a good pen.
The number of favourable outcomes for this event is the number of good pens.
Number of favourable outcomes (good pen) = 132.
The probability of drawing a good pen is:
$P(\text{good pen}) = \frac{\text{Number of good pens}}{\text{Total number of pens}}$
$P(\text{good pen}) = \frac{132}{144}$
Simplify the fraction. Both 132 and 144 are divisible by 12.
$\frac{132 \div 12}{144 \div 12} = \frac{11}{12}$
$P(\text{good pen}) = \frac{11}{12}$
Answer:
The probability that the pen taken out is a good one is $\mathbf{\frac{11}{12}}$.
Question 17. (i) A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective ?
Answer:
Given:
Total number of bulbs in the lot = 20.
Number of defective bulbs = 4.
To Find:
(i) The probability that a randomly drawn bulb is defective.
(ii) The probability that a second randomly drawn bulb (from the rest, after a non-defective bulb was drawn first and not replaced) is not defective.
Solution:
Number of good bulbs = Total bulbs - Number of defective bulbs
Number of good bulbs = $20 - 4 = 16$.
Total number of possible outcomes when drawing one bulb = 20.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability that the first bulb drawn is defective:
The event is drawing a defective bulb.
Number of favourable outcomes (defective) = 4.
The probability of drawing a defective bulb is:
$P(\text{defective}) = \frac{\text{Number of defective bulbs}}{\text{Total number of bulbs}}$
$P(\text{defective}) = \frac{4}{20}$
Simplify the fraction by dividing numerator and denominator by 4.
$P(\text{defective}) = \frac{\cancel{4}^{1}}{\cancel{20}_{5}}$
$P(\text{defective}) = \frac{1}{5}$
(ii) Probability that the second bulb is not defective (given the first was not defective and not replaced):
In the first draw, a bulb that is *not* defective (i.e., a good bulb) was drawn, and it was not replaced.
Initial number of good bulbs = 16.
After drawing one good bulb, the number of good bulbs remaining = $16 - 1 = 15$.
The number of defective bulbs remains the same = 4.
The total number of bulbs remaining in the lot = (Total initial bulbs) - 1
Total number of bulbs remaining = $20 - 1 = 19$.
Now, a second bulb is drawn at random from these 19 bulbs.
The total number of possible outcomes for the second draw is 19.
The event is that this second bulb is not defective.
The number of favourable outcomes for this event is the number of good bulbs remaining.
Number of favourable outcomes (not defective in second draw) = 15.
The probability of drawing a non-defective bulb in the second draw (given the condition) is:
$P(\text{not defective second} | \text{not defective first}) = \frac{\text{Number of good bulbs remaining}}{\text{Total number of bulbs remaining}}$
$P(\text{not defective second} | \text{not defective first}) = \frac{15}{19}$
Answer:
(i) The probability that the first bulb drawn is defective is $\mathbf{\frac{1}{5}}$.
(ii) The probability that the second bulb is not defective (given the first was not defective and not replaced) is $\mathbf{\frac{15}{19}}$.
Question 18. A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears
(i) a two-digit number
(ii) a perfect square number
(iii) a number divisible by 5.
Answer:
Given:
A box contains 90 discs numbered from 1 to 90.
One disc is drawn at random.
To Find:
The probability that the disc bears:
(i) a two-digit number.
(ii) a perfect square number.
(iii) a number divisible by 5.
Solution:
The numbers on the discs are $\{1, 2, 3, \dots, 90\}$.
The total number of possible outcomes when drawing one disc is 90.
Total number of possible outcomes = 90.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability of drawing a two-digit number:
The numbers from 1 to 9 are single-digit numbers.
Number of single-digit numbers = 9.
The numbers from 10 to 90 are two-digit numbers.
Number of two-digit numbers = Total numbers - Number of single-digit numbers
Number of two-digit numbers = $90 - 9 = 81$.
Number of favourable outcomes (two-digit number) = 81.
The probability of drawing a two-digit number is:
$P(\text{two-digit number}) = \frac{\text{Number of two-digit numbers}}{\text{Total number of discs}}$
$P(\text{two-digit number}) = \frac{81}{90}$
Simplify the fraction by dividing numerator and denominator by 9.
$P(\text{two-digit number}) = \frac{\cancel{81}^{9}}{\cancel{90}_{10}}$
$P(\text{two-digit number}) = \frac{9}{10}$
(ii) Probability of drawing a perfect square number:
A perfect square number is an integer that is the square of an integer.
The perfect square numbers between 1 and 90 are:
$1^2=1$
$2^2=4$
$3^2=9$
$4^2=16$
$5^2=25$
$6^2=36$
$7^2=49$
$8^2=64$
$9^2=81$
The next perfect square is $10^2=100$, which is greater than 90.
The perfect square numbers are $\{1, 4, 9, 16, 25, 36, 49, 64, 81\}$.
Number of favourable outcomes (perfect square) = 9.
The probability of drawing a perfect square number is:
$P(\text{perfect square}) = \frac{\text{Number of perfect squares}}{\text{Total number of discs}}$
$P(\text{perfect square}) = \frac{9}{90}$
Simplify the fraction by dividing numerator and denominator by 9.
$P(\text{perfect square}) = \frac{\cancel{9}^{1}}{\cancel{90}_{10}}$
$P(\text{perfect square}) = \frac{1}{10}$
(iii) Probability of drawing a number divisible by 5:
The numbers between 1 and 90 that are divisible by 5 are the multiples of 5.
These numbers are $\{5, 10, 15, \dots, 90\}$.
To find the number of such numbers, we can divide the last number by 5: $90 \div 5 = 18$.
So, there are 18 numbers divisible by 5 between 1 and 90.
Number of favourable outcomes (divisible by 5) = 18.
The probability of drawing a number divisible by 5 is:
$P(\text{divisible by 5}) = \frac{\text{Number of discs divisible by 5}}{\text{Total number of discs}}$
$P(\text{divisible by 5}) = \frac{18}{90}$
Simplify the fraction by dividing numerator and denominator by 18.
$P(\text{divisible by 5}) = \frac{\cancel{18}^{1}}{\cancel{90}_{5}}$
$P(\text{divisible by 5}) = \frac{1}{5}$
Answer:
(i) The probability that it bears a two-digit number is $\mathbf{\frac{9}{10}}$.
(ii) The probability that it bears a perfect square number is $\mathbf{\frac{1}{10}}$.
(iii) The probability that it bears a number divisible by 5 is $\mathbf{\frac{1}{5}}$.
Question 19. A child has a die whose six faces show the letters as given below:

The die is thrown once. What is the probability of getting
(i) A?
(ii) D?
Answer:
Given:
A die with six faces showing the letters: A, B, C, D, E, A.
The die is thrown once.
To Find:
(i) The probability of getting the letter A.
(ii) The probability of getting the letter D.
Solution:
The letters on the six faces of the die are A, B, C, D, E, A.
The total number of possible outcomes when the die is thrown once is the number of faces on the die, which is 6.
Total number of possible outcomes = 6.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability of getting A:
Let E$_{1}$ be the event of getting the letter A.
The letter A appears on 2 faces of the die.
Number of favourable outcomes for E$_{1}$ (A) = 2.
The probability of getting A is:
$P(E_{1}) = P(\text{A}) = \frac{\text{Number of faces with A}}{\text{Total number of faces}}$
$P(\text{A}) = \frac{2}{6}$
Simplify the fraction by dividing the numerator and denominator by 2.
$P(\text{A}) = \frac{\cancel{2}^{1}}{\cancel{6}_{3}}$
$P(\text{A}) = \frac{1}{3}$
(ii) Probability of getting D:
Let E$_{2}$ be the event of getting the letter D.
The letter D appears on 1 face of the die.
Number of favourable outcomes for E$_{2}$ (D) = 1.
The probability of getting D is:
$P(E_{2}) = P(\text{D}) = \frac{\text{Number of faces with D}}{\text{Total number of faces}}$
$P(\text{D}) = \frac{1}{6}$
Answer:
(i) The probability of getting A is $\mathbf{\frac{1}{3}}$.
(ii) The probability of getting D is $\mathbf{\frac{1}{6}}$.
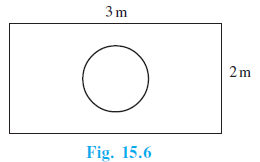
Question 20. Suppose you drop a die at random on the rectangular region shown in Fig. 15.6. What is the probability that it will land inside the circle with diameter 1m?
Answer:
Given:
A rectangular region with dimensions 3 m by 2 m.
A circle inside the rectangle with diameter 1 m.
A die is dropped at random on the rectangular region.
To Find:
The probability that the die will land inside the circle.
Solution:
This is a geometric probability problem, where the probability is determined by the ratio of areas.
The sample space is the entire rectangular region. The area of the rectangular region is the total possible area where the die can land.
Area of rectangle = length $\times$ width
Area of rectangle = $3 \text{ m} \times 2 \text{ m} = 6$ square m.
The favourable event is that the die lands inside the circle. The area of the circle is the favourable area.
The diameter of the circle is 1 m. The radius of the circle is half of the diameter.
Radius of circle, $r = \frac{1}{2}$ m.
Area of circle = $\pi r^2$
Area of circle = $\pi \left(\frac{1}{2}\right)^2 = \pi \times \frac{1}{4} = \frac{\pi}{4}$ square m.
The probability that the die lands inside the circle is the ratio of the area of the circle to the area of the rectangular region.
Probability (lands inside circle) = $\frac{\text{Area of circle}}{\text{Area of rectangle}}$
Probability (lands inside circle) = $\frac{\frac{\pi}{4} \text{ m}^2}{6 \text{ m}^2}$
Probability (lands inside circle) = $\frac{\pi/4}{6}$
To simplify the fraction, we can write:
$\frac{\pi/4}{6} = \frac{\pi}{4} \times \frac{1}{6} = \frac{\pi}{24}$
Answer:
The probability that the die will land inside the circle is $\mathbf{\frac{\pi}{24}}$.
Question 21. A lot consists of 144 ball pens of which 20 are defective and the others are good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that
(i) She will buy it ?
(ii) She will not buy it ?
Answer:
Given:
Total number of ball pens in the lot = 144.
Number of defective pens = 20.
To Find:
(i) The probability that Nuri will buy the pen.
(ii) The probability that Nuri will not buy the pen.
Solution:
First, calculate the number of good pens in the lot.
Number of good pens = Total number of pens - Number of defective pens
Number of good pens = $144 - 20 = 124$.
When the shopkeeper draws one pen at random, the total number of possible outcomes is the total number of pens, which is 144.
Total number of possible outcomes = 144.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability that she will buy it:
Nuri will buy a pen if and only if it is good.
The event is drawing a good pen.
The number of favourable outcomes for this event is the number of good pens.
Number of favourable outcomes (good pen) = 124.
The probability that she will buy the pen is:
$P(\text{she will buy}) = P(\text{good pen}) = \frac{\text{Number of good pens}}{\text{Total number of pens}}$
$P(\text{she will buy}) = \frac{124}{144}$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor, which is 4.
$P(\text{she will buy}) = \frac{\cancel{124}^{31}}{\cancel{144}_{36}}$
$P(\text{she will buy}) = \frac{31}{36}$
(ii) Probability that she will not buy it:
Nuri will not buy a pen if and only if it is defective.
The event is drawing a defective pen.
The number of favourable outcomes for this event is the number of defective pens.
Number of favourable outcomes (defective pen) = 20.
The probability that she will not buy the pen is:
$P(\text{she will not buy}) = P(\text{defective pen}) = \frac{\text{Number of defective pens}}{\text{Total number of pens}}$
$P(\text{she will not buy}) = \frac{20}{144}$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor, which is 4.
$P(\text{she will not buy}) = \frac{\cancel{20}^{5}}{\cancel{144}_{36}}$
$P(\text{she will not buy}) = \frac{5}{36}$
Alternate Solution for (ii):
The event "she will buy the pen" and the event "she will not buy the pen" are complementary events.
Using the complementary event formula: $P(\text{she will not buy}) = 1 - P(\text{she will buy})$.
From part (i), we found $P(\text{she will buy}) = \frac{31}{36}$.
So, $P(\text{she will not buy}) = 1 - \frac{31}{36}$
$P(\text{she will not buy}) = \frac{36}{36} - \frac{31}{36}$
$P(\text{she will not buy}) = \frac{36-31}{36}$
$P(\text{she will not buy}) = \frac{5}{36}$
This confirms the result obtained earlier.
Answer:
(i) The probability that she will buy it is $\mathbf{\frac{31}{36}}$.
(ii) The probability that she will not buy it is $\mathbf{\frac{5}{36}}$.
Question 22. Refer to Example 13.
(i) Complete the following table:
| Event: Sum on 2 dice | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Probability | $\frac{1}{36}$ | $\frac{5}{36}$ | $\frac{1}{36}$ |
(ii) A student argues that ‘there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability $\frac{1}{11}$ Do you agree with this argument? Justify your answer.
Answer:
Given:
Two dice, one blue and one grey, are thrown simultaneously. The possible sums of the numbers appearing on the top faces range from 2 to 12.
Solution:
The sample space when two dice are thrown consists of 36 equally likely outcomes, as listed in Example 13:
$S = \{$
$(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),$
$(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),$
$(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),$
$(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),$
$(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),$
$(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)$
$\}$
Total number of outcomes = 36.
The number of outcomes that result in a specific sum is the count of pairs from the sample space that add up to that sum.
(i) Complete the following table:
Let's find the number of favourable outcomes for each sum:
Sum = 2: (1,1) - 1 outcome. $P(\text{Sum}=2) = \frac{1}{36}$.
Sum = 3: (1,2), (2,1) - 2 outcomes. $P(\text{Sum}=3) = \frac{2}{36} = \frac{1}{18}$.
Sum = 4: (1,3), (2,2), (3,1) - 3 outcomes. $P(\text{Sum}=4) = \frac{3}{36} = \frac{1}{12}$.
Sum = 5: (1,4), (2,3), (3,2), (4,1) - 4 outcomes. $P(\text{Sum}=5) = \frac{4}{36} = \frac{1}{9}$.
Sum = 6: (1,5), (2,4), (3,3), (4,2), (5,1) - 5 outcomes. $P(\text{Sum}=6) = \frac{5}{36}$.
Sum = 7: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1) - 6 outcomes. $P(\text{Sum}=7) = \frac{6}{36} = \frac{1}{6}$.
Sum = 8: (2,6), (3,5), (4,4), (5,3), (6,2) - 5 outcomes. $P(\text{Sum}=8) = \frac{5}{36}$ (given).
Sum = 9: (3,6), (4,5), (5,4), (6,3) - 4 outcomes. $P(\text{Sum}=9) = \frac{4}{36} = \frac{1}{9}$.
Sum = 10: (4,6), (5,5), (6,4) - 3 outcomes. $P(\text{Sum}=10) = \frac{3}{36} = \frac{1}{12}$.
Sum = 11: (5,6), (6,5) - 2 outcomes. $P(\text{Sum}=11) = \frac{2}{36} = \frac{1}{18}$.
Sum = 12: (6,6) - 1 outcome. $P(\text{Sum}=12) = \frac{1}{36}$ (given).
Completed table:
| Event: Sum on 2 dice | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Probability | $\frac{1}{36}$ | $\frac{2}{36}$ | $\frac{3}{36}$ | $\frac{4}{36}$ | $\frac{5}{36}$ | $\frac{6}{36}$ | $\frac{5}{36}$ | $\frac{4}{36}$ | $\frac{3}{36}$ | $\frac{2}{36}$ | $\frac{1}{36}$ |
(ii) Do you agree with this argument? Justify your answer.
The argument is that since there are 11 possible sums (2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12), each sum has a probability of $\frac{1}{11}$.
I do not agree with this argument.
Justification:
The argument is incorrect because the 11 possible outcomes (the sums) are not equally likely.
For outcomes to be equally likely, each outcome must have the same probability of occurring.
When rolling two dice, the elementary outcomes are the 36 pairs $(x, y)$, where $x$ and $y$ are the numbers on the individual dice. Each of these 36 elementary outcomes has a probability of $\frac{1}{36}$.
The sum of the two numbers is a derived outcome, and different sums can be obtained in a different number of ways (as shown in the table above).
For example, the sum of 2 occurs in only 1 way ((1,1)), so its probability is $\frac{1}{36}$.
The sum of 7 occurs in 6 ways ((1,6), (2,5), (3,4), (4,3), (5,2), (6,1)), so its probability is $\frac{6}{36} = \frac{1}{6}$.
Since $\frac{1}{36} \neq \frac{1}{6}$, the sum outcomes are not equally likely.
Therefore, it is incorrect to assume that each sum has a probability of $\frac{1}{11}$. The probability depends on the number of elementary outcomes that result in that sum.
Question 23. A game consists of tossing a one rupee coin 3 times and noting its outcome each time. Hanif wins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
Answer:
Given:
A one rupee coin is tossed 3 times.
Hanif wins if the outcome is three heads (HHH) or three tails (TTT).
Hanif loses otherwise.
To Find:
The probability that Hanif will lose the game.
Solution:
When a coin is tossed 3 times, the possible outcomes for the sequence of results are:
H for Head, T for Tail.
The sample space S is the set of all possible outcomes:
$S = \{\text{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}\}$
The total number of possible outcomes is the number of elements in the sample space.
Total number of outcomes = $|S| = 8$.
Hanif wins if the result is HHH or TTT.
Let W be the event that Hanif wins.
The favourable outcomes for W are $\{$HHH, TTT$\}$.
Number of favourable outcomes for W = 2.
Hanif loses if the outcome is not HHH and not TTT. This is the complementary event to winning.
Let L be the event that Hanif loses.
The favourable outcomes for L are the outcomes in S that are not in W:
$L = \{\text{HHT, HTH, THH, HTT, THT, TTH}\}$
Number of favourable outcomes for L = 6.
The probability of an event is given by the formula:
$P(\text{event}) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
The probability that Hanif will lose the game is:
$P(\text{Hanif loses}) = \frac{\text{Number of outcomes where Hanif loses}}{\text{Total number of possible outcomes}}$
$P(\text{Hanif loses}) = \frac{6}{8}$
Simplify the fraction by dividing the numerator and denominator by 2:
$P(\text{Hanif loses}) = \frac{\cancel{6}^{3}}{\cancel{8}_{4}}$
$P(\text{Hanif loses}) = \frac{3}{4}$
Alternate Solution:
The event that Hanif loses is the complement of the event that Hanif wins.
The probability that Hanif wins is:
$P(\text{Hanif wins}) = \frac{\text{Number of outcomes where Hanif wins}}{\text{Total number of possible outcomes}} = \frac{2}{8} = \frac{1}{4}$
The probability that Hanif loses is $1$ minus the probability that Hanif wins:
$P(\text{Hanif loses}) = 1 - P(\text{Hanif wins})$
$P(\text{Hanif loses}) = 1 - \frac{1}{4}$
$P(\text{Hanif loses}) = \frac{4}{4} - \frac{1}{4} = \frac{3}{4}$
Both methods give the same result.
Answer:
The probability that Hanif will lose the game is $\mathbf{\frac{3}{4}}$.
Question 24. A die is thrown twice. What is the probability that
(i) 5 will not come up either time?
(ii) 5 will come up at least once?
[Hint: Throwing a die twice and throwing two dice simultaneously are treated as the same experiment]
Answer:
Given:
A die is thrown twice.
To Find:
(i) The probability that 5 will not come up either time.
(ii) The probability that 5 will come up at least once.
Solution:
When a die is thrown twice, the outcome is an ordered pair $(x, y)$, where $x$ is the result of the first throw and $y$ is the result of the second throw. Both $x$ and $y$ can be any integer from 1 to 6.
The sample space S is the set of all possible outcomes:
$S = \{(1,1), (1,2), (1,3), (1,4), (1,5), (1,6),$
$(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),$
$(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),$
$(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),$
$(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),$
$(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)\}$
The total number of possible outcomes is $6 \times 6 = 36$.
Total number of possible outcomes = 36.
The probability of an event E is given by the formula:
$P(E) = \frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
(i) Probability that 5 will not come up either time:
Let E$_{1}$ be the event that 5 does not come up on the first throw AND 5 does not come up on the second throw.
For the first throw, the possible outcomes are $\{1, 2, 3, 4, 6\}$. There are 5 such outcomes.
For the second throw, the possible outcomes are $\{1, 2, 3, 4, 6\}$. There are 5 such outcomes.
The number of outcomes where 5 does not come up either time is the product of the number of possibilities for each throw.
Number of favourable outcomes for E$_{1}$ = $5 \times 5 = 25$.
The probability of event E$_{1}$ is:
$P(E_{1}) = P(\text{5 will not come up either time}) = \frac{\text{Number of outcomes with no 5}}{\text{Total number of outcomes}}$
$P(\text{5 will not come up either time}) = \frac{25}{36}$
(ii) Probability that 5 will come up at least once:
Let E$_{2}$ be the event that 5 will come up at least once. This means 5 comes up on the first throw, or on the second throw, or on both throws.
The outcomes where 5 comes up at least once are the outcomes in the sample space where either the first coordinate is 5 or the second coordinate is 5 (or both).
Outcomes with 5 on the first throw: $\{(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)\}$ (6 outcomes).
Outcomes with 5 on the second throw: $\{(1,5), (2,5), (3,5), (4,5), (6,5)\}$ (5 outcomes - note that (5,5) is already counted in the first set).
The set of favourable outcomes for E$_{2}$ is $\{(1,5), (2,5), (3,5), (4,5), (5,5), (6,5), (5,1), (5,2), (5,3), (5,4), (5,6)\}$.
Number of favourable outcomes for E$_{2}$ = $6 + 5 = 11$.
The probability of event E$_{2}$ is:
$P(E_{2}) = P(\text{5 will come up at least once}) = \frac{\text{Number of outcomes with at least one 5}}{\text{Total number of outcomes}}$
$P(\text{5 will come up at least once}) = \frac{11}{36}$
Alternate Solution for (ii):
The event "5 will come up at least once" is the complementary event to "5 will not come up either time".
Let E be the event "5 will come up at least once".
Let $\bar{E}$ be the event "5 will not come up either time".
Using the complementary event formula: $P(E) + P(\bar{E}) = 1$.
From part (i), we found $P(\bar{E}) = P(\text{5 will not come up either time}) = \frac{25}{36}$.
So, $P(\text{5 will come up at least once}) = 1 - P(\text{5 will not come up either time})$
$P(\text{5 will come up at least once}) = 1 - \frac{25}{36}$
$P(\text{5 will come up at least once}) = \frac{36}{36} - \frac{25}{36}$
$P(\text{5 will come up at least once}) = \frac{36-25}{36}$
$P(\text{5 will come up at least once}) = \frac{11}{36}$
This confirms the result obtained earlier.
Answer:
(i) The probability that 5 will not come up either time is $\mathbf{\frac{25}{36}}$.
(ii) The probability that 5 will come up at least once is $\mathbf{\frac{11}{36}}$.
Question 25. Which of the following arguments are correct and which are not correct? Give reasons for your answer.
(i) If two coins are tossed simultaneously there are three possible outcomes—two heads, two tails or one of each. Therefore, for each of these outcomes, the probability is $\frac{1}{3}$ .
(ii) If a die is thrown, there are two possible outcomes—an odd number or an even number. Therefore, the probability of getting an odd number is $\frac{1}{2}$ .
Answer:
(i) Analysis of the first argument:
The argument is incorrect.
Reason:
When two coins are tossed simultaneously, the complete set of elementary outcomes (the sample space) is:
$S = \{\text{HH, HT, TH, TT}\}$
Here, HH means Head on both coins, HT means Head on the first and Tail on the second, TH means Tail on the first and Head on the second, and TT means Tail on both.
There are 4 possible outcomes, and each of these is equally likely, with a probability of $\frac{1}{4}$.
The argument groups these four outcomes into three categories:
- "Two heads": This corresponds to the single outcome {HH}. Its probability is $P(\text{Two heads}) = \frac{1}{4}$.
- "Two tails": This corresponds to the single outcome {TT}. Its probability is $P(\text{Two tails}) = \frac{1}{4}$.
- "One of each": This corresponds to two outcomes, {HT, TH}. Its probability is $P(\text{One of each}) = P(\text{HT}) + P(\text{TH}) = \frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2}$.
The argument is flawed because the three outcomes it lists ("two heads", "two tails", "one of each") are not equally likely. The probability can only be calculated as $\frac{1}{\text{number of outcomes}}$ if all outcomes are equally likely. Since the probabilities are $\frac{1}{4}$, $\frac{1}{4}$, and $\frac{1}{2}$ respectively, the claim that each has a probability of $\frac{1}{3}$ is incorrect.
(ii) Analysis of the second argument:
The argument is correct.
Reason:
When a fair die is thrown, the sample space of all possible elementary outcomes is:
$S = \{1, 2, 3, 4, 5, 6\}$
There are 6 equally likely outcomes.
The argument considers two possible outcomes: "an odd number" or "an even number". Let's analyze them:
- The event "getting an odd number" corresponds to the elementary outcomes {1, 3, 5}. There are 3 favourable outcomes.
- The event "getting an even number" corresponds to the elementary outcomes {2, 4, 6}. There are 3 favourable outcomes.
Since both events (getting an odd number and getting an even number) are composed of an equal number of elementary outcomes (3 each), they are equally likely events.
The probability of getting an odd number is:
$P(\text{odd number}) = \frac{\text{Number of odd outcomes}}{\text{Total number of outcomes}} = \frac{3}{6} = \frac{1}{2}$
The argument correctly identifies that there are two equally likely outcomes (odd or even) and correctly deduces the probability of one of them as $\frac{1}{2}$.
Exercise 15.2 (Optional)
Question 1. Two customers Shyam and Ekta are visiting a particular shop in the same week (Tuesday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on
(i) the same day?
(ii) consecutive days?
(iii) different days?
Answer:
Given:
Two customers, Shyam and Ekta, visit a shop during a week that includes Tuesday, Wednesday, Thursday, Friday, and Saturday.
The total number of days available for a visit is 5.
To Find:
The probability that both will visit the shop on:
(i) the same day
(ii) consecutive days
(iii) different days
Solution:
First, we need to determine the total number of possible outcomes for their visits.
Shyam can visit the shop on any of the 5 days.
Ekta can also visit the shop on any of the 5 days.
Since the visit of one person is independent of the other, the total number of possible outcomes (combinations of visiting days) is:
Total number of outcomes = (Number of days Shyam can visit) $\times$ (Number of days Ekta can visit)
Total number of outcomes = $5 \times 5 = 25$.
The probability of an event is calculated as: $P(\text{Event}) = \frac{\text{Number of Favourable Outcomes}}{\text{Total Number of Possible Outcomes}}$
(i) Probability of visiting on the same day:
The favourable outcomes are when both visit on the same day. These pairs are:
(Tuesday, Tuesday), (Wednesday, Wednesday), (Thursday, Thursday), (Friday, Friday), (Saturday, Saturday).
Number of favourable outcomes = 5.
The probability that both visit on the same day is:
$P(\text{same day}) = \frac{5}{25} = \frac{\cancel{5}^1}{\cancel{25}_5} = \frac{1}{5}$
(ii) Probability of visiting on consecutive days:
Consecutive days mean one person visits on a particular day and the other person visits on the very next day. We need to consider both possibilities (Shyam visiting first, or Ekta visiting first).
The pairs of consecutive days are (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday).
Favourable outcomes where Shyam visits the day before Ekta:
{(Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday)} - 4 outcomes.
Favourable outcomes where Ekta visits the day before Shyam:
{(Wednesday, Tuesday), (Thursday, Wednesday), (Friday, Thursday), (Saturday, Friday)} - 4 outcomes.
Total number of favourable outcomes for consecutive days = $4 + 4 = 8$.
The probability that they visit on consecutive days is:
$P(\text{consecutive days}) = \frac{8}{25}$
(iii) Probability of visiting on different days:
The event "visiting on different days" is the complement of the event "visiting on the same day".
Therefore, we can use the formula for complementary events: $P(\text{Event}) = 1 - P(\text{not Event})$.
$P(\text{different days}) = 1 - P(\text{same day})$
From part (i), we know that $P(\text{same day}) = \frac{1}{5}$.
$P(\text{different days}) = 1 - \frac{1}{5} = \frac{5}{5} - \frac{1}{5} = \frac{4}{5}$
Alternate Solution for (iii):
We can also calculate this directly.
Total number of outcomes = 25.
Number of outcomes where they visit on the same day = 5 (from part i).
Number of outcomes where they visit on different days = Total outcomes - Number of outcomes on the same day
Number of favourable outcomes = $25 - 5 = 20$.
$P(\text{different days}) = \frac{20}{25} = \frac{\cancel{20}^4}{\cancel{25}_5} = \frac{4}{5}$
Question 2. A die is numbered in such a way that its faces show the numbers 1, 2, 2, 3, 3, 6. It is thrown two times and the total score in two throws is noted. Complete the following table which gives a few values of the total score on the two throws:
What is the probability that the total score is
(i) even?
(ii) 6?
(iii) at least 6?
Answer:
Given:
A special die with faces showing the numbers {1, 2, 2, 3, 3, 6} is thrown two times.
To Find:
First, complete the given table for the total score. Then, find the probability that the total score is:
(i) even
(ii) 6
(iii) at least 6
Solution:
Step 1: Complete the table of total scores.
The table is completed by adding the number from the first throw (column) to the number from the second throw (row).
| + | 1 | 2 | 2 | 3 | 3 | 6 |
| 1 | 2 | 3 | 3 | 4 | 4 | 7 |
| 2 | 3 | 4 | 4 | 5 | 5 | 8 |
| 2 | 3 | 4 | 4 | 5 | 5 | 8 |
| 3 | 4 | 5 | 5 | 6 | 6 | 9 |
| 3 | 4 | 5 | 5 | 6 | 6 | 9 |
| 6 | 7 | 8 | 8 | 9 | 9 | 12 |
From the completed table, we can see there are $6 \times 6 = 36$ possible outcomes for the total score.
Total number of possible outcomes = 36.
(i) Probability that the total score is even:
We count the number of even scores from the table:
{2, 4, 4, 4, 4, 8, 4, 4, 8, 4, 6, 6, 4, 6, 6, 8, 8, 12}
Number of favourable outcomes (even score) = 18.
The probability is calculated as:
$P(\text{even score}) = \frac{\text{Number of even scores}}{\text{Total number of outcomes}} = \frac{18}{36} = \frac{1}{2}$
(ii) Probability that the total score is 6:
We count the number of times the score is exactly 6 from the table:
The scores of 6 appear 4 times.
Number of favourable outcomes (score is 6) = 4.
The probability is:
$P(\text{score is 6}) = \frac{\text{Number of scores of 6}}{\text{Total number of outcomes}} = \frac{4}{36} = \frac{1}{9}$
(iii) Probability that the total score is at least 6:
"At least 6" means the score is 6 or greater ( $\ge 6$ ). We count these scores from the table:
{7, 8, 8, 6, 6, 9, 6, 6, 9, 7, 8, 8, 9, 9, 12}
Number of favourable outcomes (score $\ge 6$) = 15.
The probability is:
$P(\text{score is at least 6}) = \frac{\text{Number of scores} \ge 6}{\text{Total number of outcomes}} = \frac{15}{36}$
Simplifying the fraction by dividing the numerator and denominator by 3:
$P(\text{score is at least 6}) = \frac{5}{12}$
Question 3. A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, determine the number of blue balls in the bag.
Answer:
Given:
Number of red balls = 5.
Let the number of blue balls be B.
The probability of drawing a blue ball is double that of drawing a red ball, which can be written as $P(\text{Blue}) = 2 \times P(\text{Red})$.
To Find:
The number of blue balls in the bag (B).
Solution:
The total number of balls in the bag is the sum of the number of red balls and the number of blue balls.
Total number of balls = $5 + B$.
The probability of drawing a red ball is given by:
$P(\text{Red}) = \frac{\text{Number of red balls}}{\text{Total number of balls}} = \frac{5}{5+B}$
The probability of drawing a blue ball is given by:
$P(\text{Blue}) = \frac{\text{Number of blue balls}}{\text{Total number of balls}} = \frac{B}{5+B}$
We are given the condition:
$P(\text{Blue}) = 2 \times P(\text{Red})$
Substitute the expressions for $P(\text{Blue})$ and $P(\text{Red})$ into the equation:
$\frac{B}{5+B} = 2 \times \frac{5}{5+B}$
Simplify the right side of the equation:
$\frac{B}{5+B} = \frac{10}{5+B}$
Since B represents the number of blue balls, $B \geq 0$. Therefore, the total number of balls $5+B$ is greater than or equal to 5, and thus $5+B \neq 0$.
We can multiply both sides of the equation by $(5+B)$:
$(5+B) \times \frac{B}{5+B} = (5+B) \times \frac{10}{5+B}$
$B = 10$
Check:
If B = 10, then total balls = $5 + 10 = 15$.
$P(\text{Red}) = \frac{5}{15} = \frac{1}{3}$.
$P(\text{Blue}) = \frac{10}{15} = \frac{2}{3}$.
Is $P(\text{Blue}) = 2 \times P(\text{Red})$?
$\frac{2}{3} = 2 \times \frac{1}{3} = \frac{2}{3}$. Yes, the condition is satisfied.
Answer:
The number of blue balls in the bag is $\mathbf{10}$.
Question 4. A box contains 12 balls out of which x are black. If one ball is drawn at random from the box, what is the probability that it will be a black ball?
If 6 more black balls are put in the box, the probability of drawing a black ball is now double of what it was before. Find x.
Answer:
Given:
Initial number of balls in the box = 12.
Initial number of black balls = x.
6 more black balls are added to the box.
The new probability of drawing a black ball is double the initial probability.
To Find:
The probability of drawing a black ball initially (in terms of x).
The value of x (the initial number of black balls).
Solution:
Initially, the box contains 12 balls, and x of them are black.
Total number of possible outcomes when drawing one ball initially = 12.
The number of favourable outcomes for drawing a black ball initially = x.
The probability of drawing a black ball initially, $P_1(\text{Black})$, is:
$P_1(\text{Black}) = \frac{\text{Number of black balls}}{\text{Total number of balls}}$
$P_1(\text{Black}) = \frac{x}{12}$
Now, 6 more black balls are put into the box.
New number of black balls = $x + 6$.
New total number of balls = Initial total balls + Added black balls
New total number of balls = $12 + 6 = 18$.
The probability of drawing a black ball from the new box, $P_2(\text{Black})$, is:
$P_2(\text{Black}) = \frac{\text{New number of black balls}}{\text{New total number of balls}}$
$P_2(\text{Black}) = \frac{x+6}{18}$
According to the problem statement, the new probability of drawing a black ball is double the initial probability.
$P_2(\text{Black}) = 2 \times P_1(\text{Black})$
Substitute the expressions for the probabilities:
$\frac{x+6}{18} = 2 \times \frac{x}{12}$
... (i)
Simplify the equation:
$\frac{x+6}{18} = \frac{2x}{12}$
Simplify the fraction on the right side:
$\frac{x+6}{18} = \frac{x}{6}$
Multiply both sides by the least common multiple of 18 and 6, which is 18, to clear the denominators:
$18 \times \frac{x+6}{18} = 18 \times \frac{x}{6}$
$x+6 = 3x$
Subtract x from both sides:
$6 = 3x - x$
$6 = 2x$
Divide by 2:
$x = \frac{6}{2}$
$x = 3$
Since x represents the number of black balls, it must be a non-negative integer. Also, initially, there were 12 balls, so x must be less than or equal to 12. The value $x=3$ satisfies these conditions.
Answer:
The probability that it will be a black ball initially is $\mathbf{\frac{x}{12}}$.
The value of x is $\mathbf{3}$.
Question 5. A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is green is $\frac{2}{3}$ Find the number of blue balls in the jar.
Answer:
Given:
Total number of marbles in the jar = 24.
The marbles are either green or blue.
The probability of drawing a green marble, $P(\text{Green}) = \frac{2}{3}$.
To Find:
The number of blue marbles in the jar.
Solution:
Let the number of green marbles be $G$.
Let the number of blue marbles be $B$.
The total number of marbles in the jar is the sum of green and blue marbles:
$G + B = 24$
The probability of drawing a green marble is given by:
$P(\text{Green}) = \frac{\text{Number of green marbles}}{\text{Total number of marbles}}$
$P(\text{Green}) = \frac{G}{24}$
We are given that the probability of drawing a green marble is $\frac{2}{3}$.
So, we have the equation:
$\frac{G}{24} = \frac{2}{3}$
To find the number of green marbles ($G$), multiply both sides of the equation by 24:
$G = \frac{2}{3} \times 24$
$G = 2 \times \frac{\cancel{24}^{8}}{\cancel{3}_{1}}$
$G = 2 \times 8$
$G = 16$
So, there are 16 green marbles in the jar.
Now, using the total number of marbles:
Number of green marbles + Number of blue marbles = Total marbles
$16 + B = 24$
Subtract 16 from both sides to find the number of blue marbles:
$B = 24 - 16$
$B = 8$
Answer:
The number of blue marbles in the jar is $\mathbf{8}$.

